2021 is my sixth year at MIT. Four years as an undergraduate, one year as a masters student, and this year, a “first-year” PhD student. MIT EECS requires all PhD students to take four academic classes as part of the “technical qualifying exam” (TQE), but these classes need not be completed during the official PhD years. I passed my first TQE class in my sophomore fall, and my last one about a year ago, in the midst of quarantine. Needless to say, it’s been a while since I’ve seriously taken an academic class.
Nowadays, more and more, I find that these classes — all those sleepless nights — boil down to some underwhelming intuitions. These intuitions stick with you, when all the computations and proofs fade. You could even call them aphorisms, though tailored specifically towards a niche, machine learning audience. Regardless, here is a distillation of my revered MIT EECS education, 1% rigor and the rest, handwavy rambling.
Probability Theory (18.175)
I dropped this class after the first exam because it took 20 hours a week. While it lasted, however, it was easily one of my most eye-opening classes at MIT. We spent the first 1.5 weeks learning how to sample uniformly from 0 to 1.
Growing up, I’ve always thought of random variables as really random. You flip a coin and you don’t know which side will land face-up. Roll a die, same uncertainty. Unintuitively, there’s nothing “random” about random variables. They are measurable functions on a probability space, introduced after defining each of those words for two weeks.
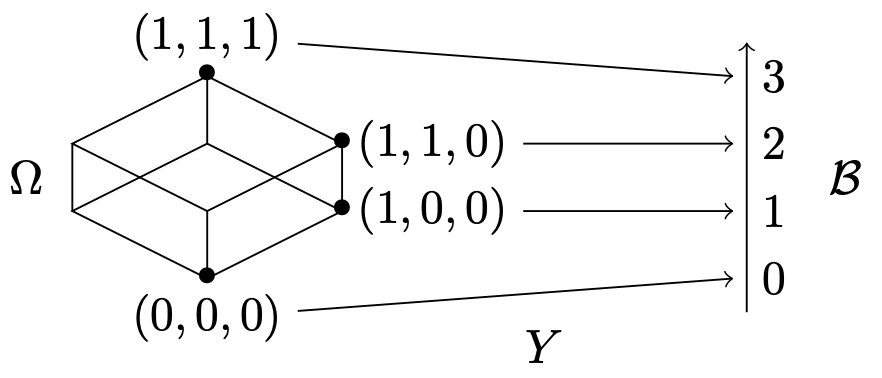
Care to decipher what this figure depicts?
In high school, we drew rectangles upwards from the $x$ axis. Lebesgue cut up the range instead.
Euler (oiler not you-ler) is a great name, but two syllables is a tad short, no? Galois and Markov are similarly out of the running. So … I raise you Kolmogorov! Ionescu Tulcea! Carathéodory! Lebesgue himself is pretty unique too: in Animal Crossing I have a villager named Henry and I changed his catchphrase to “Lebesgue!” No disrespect intended, of course.
Granted, the probability theory textbook contained these old folks, who were not contained by probability theory — if that makes any sense.
Statistics (18.650)
On day one, my statistics professor told us that these two theorems are all we need to know, for the whole semester. Truly, has anyone counted the sheer number of these things?
Note, the aphorism is not these theorems themselves; it is the idea (joke) that they suffice.
Machine Learning (6.867)
I was baited into the graduate machine learning class in my sophomore year, without most of the prerequisite knowledge, but an eagerness to prove the professors wrong. I got an A, but the professors were right — I would have benefited more from this class had I taken it a year later.
In my humble opinion, the no free lunch theorem is the most aphoristic belief held among machine learning practicioners today. Nobody bothers reading the original paper, or articulating the precise definition, but every machine learning class cites it as a central tenet.
There are some often unsaid notes associated with this idea. You can’t claim your model operates in a data-scarce regime if your validation set is a hundred times your training set. Deep learning doesn’t quite fit the “single descent” paradigm so you have to be careful about when to stop.
However, I encounter a surprising number of people who believe that their models, trained to 0.9999 saturation, are better than mine.
Bayesian Inference (6.435)
Most handwavy statement ever about exchangeability.
They are pseudo-random.
This was a wake-up call, like learning that random variables
themselves are not “random.”
It turns out that numpy.random() reads off a fixed list
(okay perhaps not so trivial, but this general idea).
Random number generators should satisfy “nice” properties,
such as producing numbers on a “lattice” structure.
However, the crux of it is reading off a list.
I scribed the first lecture, when the professor introduced mean-field variational inference. I honestly think “cloud puffs” is so cute. How many cloud puffs would you like today, oh 2D not-very-aesthetic cloud?
1 | |
Inference and Information (6.437)
It irks me to no end when I see a technical paper cite KL divergence as a “distance metric” between individual datapoints. Not naming names.
Also, all I can say is that related proofs are bashy and long, but if you don’t know how to bash the right way, tough luck. Due to COVID, the Spring 2020 term was graded on a pass/fail scale, so naturally, I paid less attention to my classes. Therefore, if you asked me to bash a divergence-related proof today, I probably could not.
For the uninitiated, this curve measures the balance true positives and false positives. People generally measure the area under this curve (ROC-AUC). Random guessing is 0.5, heavenly perfection is 1, and heavenly imperfection is 0.
During my first two years in my lab, I worked on natural language processing. The standard scores you report on papers are F1 and accuracy. When I switched to chemistry, I realized that some people in this world actually care about this (non) obscure ROC curve. Once I was training a baseline model and jumped in delight at the score of 0.1, until I realized that my metric was ROC-AUC and my code had a bug.
Computer Vision (6.869)
We had an image classification project, in which we were supposed to think of creative neural networks to classify scenes. After a couple of tries, everyone eventually realized that we should just train a ResNet architecture, copied from the Internet.
Even though we weren’t supposed to use pre-trained weights, we quickly realized that we were not going to attain SOTA by training on our laptops. For the final projects, I wrote code that technically should have worked (deep colorization), but again, no way it was going to produce decent results from my laptop.
I take GPUs for granted now, but back then, what a rude awakening!
End
That is all. Maybe I will write another post for non-ML classes, but bye for now.